
2017年3月
自古以來人們在日常生活或商品交易中,為了容易表示數量較多的物體,通常會使用一些特別單位來度量這些物體。例如古代人們用繩子串起一千個銅錢稱為「貫」,當錢的數量較多時,就以「貫」為單位來計算。現今在商店裡,鉛筆以12支為1「打」來計算;又如乒乓球1「打」和高爾夫球1「打」的價格不一樣,但其數量都一樣。再以販售白米、豆類或乾果為例,因為它們的顆粒太小,消費者購買的數量也不可能只買一粒,如果商店要標示一粒白米或綠豆的價格,也很不實際。通常會將這些白米、豆類裝成一袋或一包,買賣時以「袋」或「包」為單位出售,而不計算它們的實際數量。另有超市以一「箱」奇異果為單位販售,而火柴、雞蛋則用「盒」為單位計算。
宇宙空間,恒星間的距離太遙遠,即使以光速(3×108 m/s)的高速至少也要花上千年、萬年才能到達。因此天文科學家在表示恒星間的距離時,通常用「光年」來表示距離,因為如果用“公尺”或“公里”顯得非常不方便。
科學上,微觀世界的一個原子或分子是不容易衡量其質量的,且日常所接觸的物質,又大多由巨量的原子或分子所集合而成,而非單獨的原子或分子。因此,為了要方便處理數量很多的原子或分子,必須以較簡便的計量方式來表示它們的個數。
義大利科學家亞佛加厥於1811年提出「於相同的物理條件下,相同體積的氣體含有相同數分子」的假說,這個理論對後來科學家們在量測原子量和分子量上非常有幫助,也因而引發出「莫耳」的觀念。漸漸地科學家們在研究分子的物理化學性質時,就開始使用莫耳這個單位。用莫耳為單位來計算化學反應的分子數量非常方便,因為單獨一個原子或分子的質量無法衡量,但是一莫耳的原子或分子就可以很容易地用天平稱出。
莫耳的緣起和歷史
莫耳這個名詞最早是1893年拉脫維亞裔德國籍物理化學家奧士華 (Friedrich Wilhelm Ostwald) 以“g-Molekül”為單位來衡量物質的大小;“Molekül”是德語「分子」之意。當時他定義:當物質的質量等於其分子量時,該物質為1 mol,用以界定一個樣品的大小為具有相等於該物質式量 (formula weight) 的質量。隨後和他一起研究的電化學專家能斯特 (Walther Hermann Nernst) 將“g-Molekül”簡稱為“mol”作為式量的單位。而後又定義:當氣體在標準狀況下的體積為22.4公升時,該氣體為1 mol。
1893年“gramme-molecule”這個用語首先以英文出現在大英百科全書 (Encyclopaedia Britannica)。而英文用語“mole莫耳”第一次出現在1902年翻自奧士華著作的無機化學原理(Principles of Inorganic Chemistry) 英譯本。
1909年法國物理學家佩蘭 (Jean Baptiste Perrin) 建議使用克分子 (gram-molecule),並提出以莫耳表示實體數目。基於慣用的物質之克分子係氣態下具有和同溫同壓下2 g的氫氣相同體積的物量,他首先對亞佛加厥數 (Avogadro's number) 下了定義:任何兩個克分子含有相同分子數,而這個不變的數 (invariable number) 是一個通用常數,其可適當地指定為亞佛加厥常數。
德國物理技術研究院 (Physikalisch-Technische Bundesanstalt; PTB) 院長斯第萊(Ulrich Stille) 在1955年發表的計量教科書中,開始用“g-mole”。依據斯第萊的分析,單位莫耳(mol)在當時被用於三種的不同概念。第一種是作為「化學質量單位 (chemical mass unit),例如:「1莫耳等於22.991 g的鈉」或「1莫耳等於58.448克氯化鈉」。其次是作為一個「莫耳數(number of moles)」,例如:「在公式l = n / L中,n是樣品中的實體數,L是亞佛加厥數。第三種用法是作為物質的量 (即物量,德語為Stoffmengde)。例如:「1莫耳為一個包含與原子氧Ar(O)g一樣多的實體之物量 (Stoffmengde),其中Ar(O)是氧的原子量。」
儘管科學家們很早就開始使用“莫耳”,但是對這個單位的認識卻有所不同,直到國際度量衡委員會 (CIPM) 根據國際純物理暨應用物理聯合會 (IUPAP)、國際純化學暨應用化學聯合會(IUPAC) 與國際標準化組織 (ISO) 的建議,於1967年制定了莫耳的定義,隨後在1971年第14屆國際度量衡大會才正式決定將莫耳 (mole) 列為國際單位制 (SI) 中七個基本單位之一,並對莫耳明確地給予如下定義:「莫耳等於物質系統中所含之基本實體數與質量為0.012 kg之碳-12所含原子數相等時的物量。使用莫耳時,基本實體應予以界定,可以是原子、分子、離子、電子及其他粒子,或是這些粒子的特定組合。」此定義遵循「碳-12莫耳質量是每莫耳就是12 g,M(12C) = g/mol」的原則。
CIPM的單位諮詢委員會 (Consultative Committee for Units; CCU) 1980年的報告中提及「此定義中的碳-12可理解為處於靜態及基態的非結合原子 (unbound atoms)。」此莫耳的定義亦決定了與物量實體數量相關的通用常數-亞佛加厥常數,其符號為NA或L。如果於特定樣品中X實體的數量為N(X),而n(X) 為以莫耳為單位的物量,則它們之間的關係為:
n(X) = N(X)/NA
上式中,N(X) 為無量綱,n(X) 單位為“mol”,亞佛加厥常數具有SI一貫導出單位“mol-1”。
由於莫耳的定義近似於一個數,因此莫耳是否應該成為基本單位 (base unit),一直被爭論著,這是因為數 (number) 在SI量制中無法構成一個量綱。值得注意的是莫耳當初作為基本單位之一而被國際度量衡大會引入SI單位制時,其主要目的在於解決g-mol與kg-mol在使用上的混亂;其次是將量綱分析引入化學領域。
莫耳的實用性
莫耳的定義若直接從原文翻譯上來看,比較不易理解,可以簡明解釋為:「莫耳係表示一個特定系統中某種微觀粒子 (如原子、分子等) 數量的一種單位,一莫耳微觀粒子在數量上等於12 g碳-12所含有的原子數量。特別要分辨的是莫耳不是表示質量的單位,而是表示物質所含某微觀粒子數量的單位;即物量的單位。
莫耳這個單位含有一個巨量的數目,12 g碳-12的原子經實際量測,約為6.022141×1023個,這個數也被稱為亞佛加厥常數。例如,1莫耳氧分子實際上表示的是6.022141×1023個氧分子。1莫耳的任何物質所含的粒子數是相同的,例如1莫耳碳原子含有的原子數和一莫耳氧分子含有的分子數相同。至於莫耳和12 g碳-12所含的原子數相關聯的原因是相對原子質量 (原子量)是以碳-12為標準的。國際上把相對原子量單位定義為「碳-12原子量的1/12」,即碳-12的原子量為12。如此一來,1莫耳的原子或分子的質量用g來表示時,在數值上剛好等於它們各自的原子量或分子量。換言之,1莫耳原子的質量與單個原子質量的比值就是亞佛加厥常數。例如,碳-12的原子量為12,一莫耳碳-12原子的質量為12 g;氫原子的原子量為1.008,一莫耳氫原子的質量為1.008 g。
當一位研究人員從實驗或週期表中獲知某元素的原子量或分子量,就知道了一莫耳元素的質量;1莫耳元素的質量亦稱為莫耳質量 (molar mass)。只要能準確量測出某元素的原子與碳-12原子間的相對質量比,即可得到該元素的莫耳質量,因為原子之間的相對質量比可以用質譜分析等現代量測方法準確地測得。此外,利用莫耳為單位來研究原子、分子等微觀粒子以及如熵、焓等物理化學性質時也非常方便,可以將較難計量的微觀粒子與容易計量的巨觀物質聯繫在一起;這就是為何有人稱莫耳是微觀粒子與巨觀物質之間的橋樑。
莫耳新定義
莫耳自1971年定義之後,即少有變更內的決議。不過,當有許多計量學家想針對基本量中最後一個以人工製品 (artifact) 決定的公斤 (kilogram) 進行重新定義時,一個企圖連同安培、克耳文和莫耳都一併重新定義的「新SI」方案就被提出來討論。此方案希望基本量的定義都能一致地達到明確不變的簡潔陳述,即以一個具公認正確值之基本常數來定義單位,以及用最高層級原級方法實現定義。
2011年CGPM大會中,莫耳被提議重新定義為“The mole is the unit of amount of substance of a specified elementary entity, which may be an atom, molecule, ion, electron, any other particle or a specified group of such particles, its magnitude will be set by fixing the numerical value of the Avogadro constant to be equal to exactly 6.022 14X ×1023 when it is expressed in the SI unit mol–1.”,中文可譯為:「莫耳是一個特定基本實體的物量單位,該實體可以是一個原子、分子、離子、電子、任何其他粒子,或是該等粒子的特定群組。其大小藉由固定亞佛加厥常數之數值等於6.02214X×1023,以SI單位表示為mol-1。」
其中符號X表示一個或多個附加數字,將隨著時間被實現更新。其實這些尾隨數字的正確值對任何化學量測而言,並不會有任何實際的影響。
這提議的目的雖然是為使基本單位所定義方式有一致性,也有許多論點支持固定亞佛加厥常數的數值。因為依先前的定義,1莫耳的純同位素碳-12的質量是確切知道的,每個其他元素1莫耳的質量均具有該元素原子量的不確定度。不過無法陳述1莫耳實體的確切數,雖然其為亞佛加厥數,而亞佛加厥數卻有不確定度。如果改採固定亞佛加厥數的新定義,則任何元素1莫耳的實體的數目將被確切知道,只是任何元素1莫耳的質量將會有不確定度,即等於該元素原子量的不確定度。此即將「物量」簡化為只是實體的數目,擺脫具有特定實體數目物質的質量的定義,而只以實體的數目來定義。
莫耳的實現
作為一個國際單位制基本單位的莫耳,怎樣才能準確實現呢?理論上說,只要準確數出12克碳-12所含的原子數量即可,然而目前的科技水準還不能將碳原子逐個分離出來,即使通過每秒一萬億次的計數器,也要用一萬九千年才能數完這麼多的原子。但是科學家可以利用其他的物理、化學方法比較準確地測出亞佛加厥常數,根據莫耳的定義,量測亞佛加厥常數就可以看成實現了莫耳單位。莫耳可用不同的原級方法(primary method)來實現。以下舉出幾個例子說明:
1. 對於純淨樣品 (pure sample) 而言,物量n在樣品中的量可經由天秤量測出樣品的質量m,再除以莫耳質量 (molar mass) M而得到,其公式為
n = m/M
式中m為質量 (g),M為莫耳質量 (g /mol),n為物量 (mol)。莫耳質量很容易地從元素週期表算出任何純淨化合物的化學式。天然同位素組成之元素的莫耳質量係從分子量(即相對分子質量) 乘以單位“g /mol” 得到的。莫耳質量的所有核種 (nuclide) 是已知且具10-7或更小的相對標準不確定度,有許多元素甚至小於10-8。
實現莫耳的方法通常利用最精密的方法,因為量測樣品的質量是一個相對簡單而準確的方法。用這種方法,莫耳可容易地被實現而具有小於1×10-6的相對標準不確定度。然而,值得注意的是這程序取決於須有純淨材料的樣品,這意味著要有樣品的精密化學分析,因為這是不確定度評估的限制因素。
2. 對於純淨氣體而言,物量可以從下面的氣體狀態方程式來計算出:
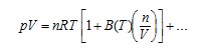
式中P為壓力,V為體積,T為溫度,R為莫耳氣體常數8.3144598 J/(mol·K)。此式包含第二均功係數 (virial coefficient) B(T) 和可能更高的第三均功係數,這是一項小的修正。為了多種目的,在壓力低於一大氣壓時,物量可以用足夠準確的理想氣體方程式計算:
![]()
莫耳氣體常數R為已知,單位為“Pa m3 mol-1 K-1”,相對標準不確定度為1.7×10-6,如此n的單位為“mol”。用這方法在量測n時,其不確定度取決於量測壓力、體積和溫度的不確定度,以及氣體不純度的修正。當然,實現這種氣體莫耳的方法也取決於所使用氣體樣品的純度。
3. 在化學電解中,一個電極上的物量n正比於通過系統所釋放的電荷Q,即電流I和其流動的時間t的乘積。比例常數是被釋放的離子數z乘以法拉第常數F的倒數,根據公式:
n = zQ / F = zIt / F
式中法拉第常數F為已知,單位為“C/mol”相對標準不確定度為2.5×10-8,如此n的單位為“mol”。
莫耳實現的新方法
目前國際上由CODATA推薦的值約為6.022141×1023。隨著科學的進步和量測技術的提高,亞佛加厥常數正被不斷地修正,計量科學家們追求的目標是能更準確實現莫耳的新方法;如通過x射線繞射量測矽單晶的密度方法等。由於亞佛加厥常數的值等於質量0.012 kg的碳-12所具有的原子數。量測此原子數必須用碳-12的單晶體量測原子的質量、密度和原子間距。近年來世界各先進計量研究機構紛紛採用矽來代替碳-12,因為矽可製成大塊無雜質的純單晶其純度可達到99.99%。為了得到這個值,還必須用質譜儀量測碳-12與矽的原子量之比值以及矽的同位素成分。
此一較新穎的方法係採用雷射干涉儀量測近乎理想球體的矽晶球直徑,由此算出矽晶球的體積和密度,並稱出其質量;這種方法的困難是量測晶格常數。科學家利用X射線干涉儀通過晶體的晶格產生繞射,可以求出晶體晶格間距和X射線波長的倍數關係。如用可量測小位移的X射線和光學干涉儀即能直接量測矽晶體的晶格常數。這種方法量測矽晶體晶格距離的相對誤差已達到3.5×10-4,而亞佛加厥常數的不確定度也相對減少至3.0×10-8。
