






2017年8月
國際單位制SI
一個量的值Q可用一個數{Q}和一個單位[Q]的乘積表示:
Q = {Q}[Q]
「單位」是量值的特定實例,依約定而定義,它是用來作為一個參考 (reference),而「數」是量值對單位的比例數;例如{6}為量值6 kg對單位[kg]的比例,即{Q} = Q/[Q]。對於一個特定的量,可以使用不同的單位;例如粒子速度v的值可以表示為v = 25 m/s或v = 90 km/h,其中米每秒 (m/s) 與公里每小時 (km/h) 為速度量值相同之可交換的單位。當「量」的量測結果發表時,受測量 (被量測的量) 的估計值與該值的相關不確定度是必要的。兩者都以相同的單位表示。
1. SI的基本定義常數
一個基本常數的值像任何量一樣,亦可用一個數與一個單位的乘積表示,即Q = {Q}[Q]。此處,Q表示常數的值,當它的單元以[Q]表示時,{Q}表示其數值。例如,在真空中的光速是自然常數,以c表示,其值在SI單位以下式表示:
c = {c} [c] = 299 792 458 m/s
其中數值{c} = 299 792 458,單位[c] = m/s。
以相應的SI單位表示時,常數之值的定義即由每個常數的確切數值 (exact numerical value) 所指定。通過固定的確切數值,單位即被明確界定;如此,數值{Q}和單位[Q]的乘積應等於常數的量值Q,這是假設Q的值不會變。
採用這樣的方式選擇7個物理常數,使SI中的任何單位可用一個定義常數 (defining constant) 本身,或定義常數的乘積或比率來描述。BIPM在2016年公布所選取的7個定義常數中,新採用4個物理常數作為定義常數:
普朗克常數h:6.626 070 040 × 10-34 J s,
基本電荷e:1.602 176 620 8 × 10-19 C,
波茲曼常數k:1.380 648 52 × 10-23 J/K,
亞佛加厥常數NA:6.022 140 857 × 1023 mol-1,
另外,現有之3個物理常數仍未作變換:
銫133原子於未擾動的基態超精細分裂頻率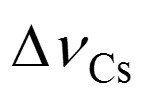 :9 192 631 770 Hz,
:9 192 631 770 Hz,
光在真空中的速度c:299 792 458 m/s,
頻率540 × 1012 Hz之單色輻射光的發光效能:683 lm/W,
保持連續性為SI於任何改變時的基本特色,並在所有定義改變時仍一直有保證。因此,只要在科學的進步和知識允許範圍內,定義常數的數值被選擇和先前的定義一致,其數值沒有不確定度。
新定義使用導出單位焦耳 (J)、庫倫 (C)、赫芝 (Hz)、流明 (lm) 及瓦特 (W) 表達之上述7個定義常數的單位,若以基本單位表達,則如表一,其中Sr為無量綱單位立弳 (steradian)。
表一 SI新7個定義常數與相應7個單位的定義
| 定義常數 | 符號 | 數值 | 單位 |
|---|---|---|---|
| 銫133超精細分裂頻率 | 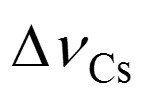 |
9 192 631 770 | Hz = s−1 |
| 光在真空中的速度 | c | 299 792 458 | m s−1 |
| 普朗克常數 | h | 6.626 070 040 × 10−34 | J s = kg m2 s−1 |
| 基本電荷 | e | 1.602 176 620 8 × 10−19 | C = A s |
| 波茲曼常數 | k | 1.380 648 52 × 10−23 | J K−1 = kg m2 s−2 K−1 |
| 亞佛加厥常數 | NA | 6.022 140 857 × 1023 | mol−1 |
| 發光效能 | Kcd | 683 | lm W−1 = kg-1 m-2 s3 cd sr |
2. 定義常數的性質
定義常數的性質列於自然基本常數到技術常數之間。利用常數以定義單位,隔開單位的定義和實現。如此,可隨著技術的發展,開發出完全不同或更出色的實際實現,而不須要變更定義。
像Kcd這技術常數涉及到特殊的應用。其原則上可以自由選擇,例如包括生理學或其他約定的加權因子。相較之下,一般自然基本常數不會賦予這種選擇,但它會通過物理方程式關聯至其他常數。
選擇這組七個定義常數係因能提供一個基本又穩定的通用參考基準,同時可為最小不確定度的實際實現。技術約定和規範還需考量歷史的發展。
普朗克常數h和光在真空中的速度c兩者基本常數,分別用以決定量子效應和時空特性,並在任何標度和環境中對所有粒子和場都有同樣的影響。
基本電荷e對應於藉由精細結構常數α = e2/ (2ce0h) 的電磁力的耦合強度,其中e0是電量常數。一些理論預測α隨時間而變化。不過α最大可能變化的實驗界限非常微小,畢竟在可預見的實際量測上,α所造成的任何影響均可被排除。
波茲曼常數k對應於溫度 (單位克耳文) 和能量 (單位焦耳) 之間的換算因子 (conversion factor),其數值係取自溫標上之歷史規格。系統的溫度與熱能有比例關係,但不必然與系統的內能有關係。在統計物理上,波茲曼常數藉由量子力學可及態的數W 和熵S相關連,S = k ln W.。此式描述系統的微觀條件 (Ω) 和宏觀狀態 (S) 之間的關係,是統計物理的一個中心概念。
銫-133原子的非擾動基態超精細分裂的頻率 (銫頻率) ,具有原子參數的特性,會受環境(如電磁場)的影響。然而,這種躍遷是很好理解的,不只穩定,而且在實際的考量下,作為參考躍遷是一個不錯的選擇。如銫頻率 之原子參數的選擇,並未如h、c、e或k分開定義和實現。
亞佛加厥常數NA對應於物量單位 (單位莫耳) 與計算實體的單位 (單位為1) 之間的換算因子。因此,它具有與波茲曼常數k相似之比例常數的特性。
發光效能Kcd是與人眼的約定光譜響應相關之技術常數。
SI基本單位的新定義及其影響
SI基本單位的名稱和符號及所對應之基本量如表二。CIPM所提之以定義常數為基礎的SI基本單位新定義,目前仍未正式確定 (預定在2018年CGPM大會決定),現僅就所提之新定義內容及其影響,分別作介紹:
表二 SI基本單位名稱與符號
| 基本量 | SI基本單位 | ||
| 名稱 | 符號 | 名稱 | 符號 |
| 長度 (length) | l, x, r,等 | 米 (meter) | m |
| 質量 (mass) | m | 千克 (kilogram) | kg |
| 時間 (time) | t | 秒 (second) | s |
| 電流 (electric current) | I, i | 安培 (ampere) | A |
| 熱力學溫度 (thermodynamic temperature) | T | 克耳文 (kelvin) | K |
| 物量 (amount of substance) | n | 莫耳 (mole) | mol |
| 光強度 (luminous intensity) | Iv | 燭光 (candela) | cd |
1. 秒的新定義
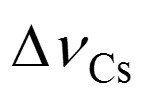 = 9 192 631 770 Hz。倒過來看該關係時,單位秒的表達式由定義常數
= 9 192 631 770 Hz。倒過來看該關係時,單位秒的表達式由定義常數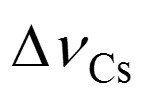 給出:
給出: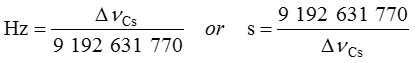
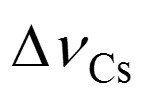 所定義。
所定義。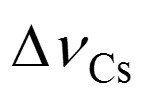 給出:
給出: 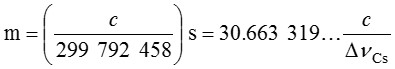
這定義的效應為:1米為光在真空中於為期299 792 458分之1秒的時間間隔內所行經之長度。
3. 千克的新定義
千克的新定義和現行的定義有根本上的變化。現行的定義是國際千克原器m(K) 的質量,新定義則是經由普朗克常數,連結至光子所具有的能量與質量當量。
千克係質量之SI單位,符號為kg。其由普朗克常數h之選取固定數值所定義,以J s為單位 (即kg m2 s–1) 時,其值為6.626 070 040 × 10-34,其中米和秒分別由c和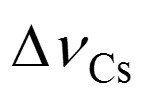 所定義。
所定義。
這定義意味著確切關係h = 6.626 070 040 × 10−34 kg m2 s−1。倒過來看該關係,單位千克的精確表達式係由定義常數h、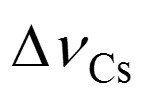 和c給出:
和c給出:
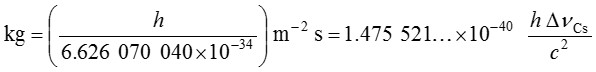
這定義的效應為:定義此一單位kg m2 s−1〔此亦為作用量 (action) 和角動量 (angular momentum) 兩個物理量的單位〕。並以普朗克常數h的值與秒和米的定義一同引導到質量的單位定義。
先前千克的定義固定於國際千克原器m(K) 的質量值,確切等於1千克,而普朗克常數(Plank constant) h的值必須通過實驗來確定。目前的定義確切地固定於h值,而原器的質量現在則必須通過實驗來確定。
在此定義中,普朗克常數所選用的數值於其被採納時,國際千克原器m(K) 的質量等於1 kg,含相對標準不確定度2.0 × 10-8,這是那時普朗克常數的值之組合最佳評估的標準不確定度。
千克的重新定義可確保千克的長期穩定度與可靠度,解決目前定義無法絕對量測的問題;此外,可在任何實驗室實現準確的千克量測,不必再依賴特定標準器。
4. 安培的新定義
安培係電流之SI單位,符號為A。其由基本電荷e之選取固定數值所定義,以C (即A s)為單位時,其值為1.602 176 620 8 × 10−19,其中秒由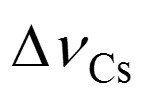 所定義。
所定義。
這定義意味著確切關係 e = 1.602 176 620 8 × 10−19 A s.。倒過來看該關係時,安培的精確表達式係由定義常數e和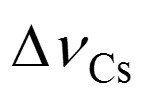 給出:
給出:
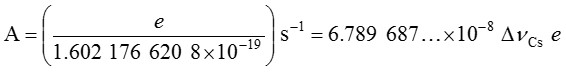
這定義的效應為:1安培係對應於每秒流過1/ (1.602 176 620 8 × 10-19) 個基本電荷的電流。
先前安培的定義係以載有電流之導體間的力為基礎,並將磁場常數 (真空磁導率) μ0的值固定於恰好4π × 10-7 H m-1 = 4π × 10-7 N A-2,H和N分別表示一貫導出單位亨利 (henry) 和牛頓 (newton)。安培的新定義係固定e的值而不是μ0,因此μ0必須通過實驗確定。
隨之而來的是必須通過實驗來確定真空介電常數ε0 =1/μ0c2、真空特性阻抗Z0 = μ0c和真空導納Y0 =1/μ0c的值,這些參數現在也受到與μ0相同的相對標準不確定度所影響,這是由於c是確切已知常數的關係。在新的安培定義上,μ0仍等於4π × 10-7 H/m,相對標準不確定度則會小於1 × 10-9。
5. 克耳文的新定義
克耳文的新定義和現行的定義有根本上的變化。現行的定義是利用水的狀態變化之溫度定義溫標,新定義則是使用波玆曼常數k表示溫度和能量。
克耳文係熱力學溫度之SI單位,符號為K。其由波玆曼常數k之選取固定數值所定義,以J K–1為單位 (即kg m2 s-2 K-1) 時,其值為1.380 648 52 × 10–23;其中千克、米和秒分別由h, c和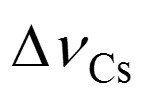 所定義。
所定義。
這定義意味著確切關係k = 1.380 648 52 × 10−23 kg m2 s-2 K-1。倒過來看這該關係,克耳文的精確表達式係由定義常數h, c和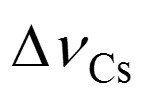 給出:
給出:
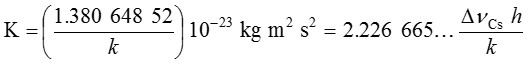
這定義的效應為:1克耳文係等於熱力學溫度的變化,導致熱能量kT的變化為1.380 648 52 × 10-23 J。現行的克耳文定義係以確切數值即選定水三相點TTPW (冰、水和水汽共存的三相點),溫度為273.16 K為基準,其只定義一個溫度點,且受水的純度、同位素含量、梯度、退火等影響。溫度新定義則不再由水的特性著手,乃是從微觀基礎上將溫度觀念與能量連結起來。因克耳文的新定義固定於波玆曼常數k的數值以取代TTPW,故後者必須通過實驗確定。在採用新定義時,TTPW等於273.16 K,含相對標準不確定度小於1 × 10-6。
6. 莫耳的新定義
莫耳的現行定義和千克有密切相關,而新定義則使莫耳為物質的實體之特定數量,中斷了這關聯性。
莫耳係一個特定基本實體的物量之SI單位,符號為mol。基本實體可以是一個原子、分子、離子、電子,任何其它粒子或這些粒子的特定群組。其由亞佛加厥常數NA之選取固定數值所定義,以mol-1為單位時,其值為6.022 140 857 × 1023。
這定義意味著確切的關係NA = 6.022 140 857 × 1023 mol-1。倒過來看該關係,單位莫耳的表達式係由此定義常數NA給出:
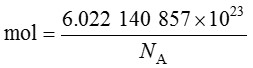
這定義的效應為:莫耳係含有6.022 140 857 × 1023個指定基本實體的系統之物量。現行莫耳的定義係固定於碳12的莫耳質量M (12C),確切等於0.012 kg/mol,而定義更新之後,M (12C) 不再是確切的已知值,必須通過實驗來確定。對於選擇NA的值之後,在採用莫耳的新定義時,M (12C) 仍於0.012 kg/mol,但含小於1 × 10-9之相對標準不確定度。
莫耳的定義更新之後,任何原子或分子的莫耳質量X仍可從其相對原子質量Ar (X) 依下式獲得:
M (X) = Ar (X) [M (12C) /12] = Ar (X) Mu
並且任何原子或分子的莫耳質量X也可由下式與基本實體m(X)質量相連結:
M (X) = NA m (X) = NA Ar (X) mu
在這些方程中,Mu是莫耳質量常數,等於M (12C) /12;mu是統一的原子質量常數,等於m (12C) /12。它們藉由亞佛加厥常數有下式的關係:
Mu = NA mu
透過連結與質量千克新定義之實現方法,可不再仰賴傳統秤重技術的物量追溯方法,降低參考物質的使用數量,同時可擴充化學分析準確定量的範圍。
7. 燭光的新定義
燭光的新定義在實質上與現行的定義相同,只是在定義敘述上略作改變而已。
燭光係給定方向光強度之SI單位,符號為cd。其由頻率540 × 1012赫茲單色輻射光的發光效能Kcd之選用固定數值所定義,以單位lm W–1 (即cd sr W–1或cd sr kg-1 m-2 s3) 表示時,其值為683;其中千克、米和秒分別由h, c和 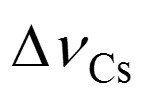 所定義。
所定義。
這定義意味著確切關係Kcd = 683 kg-1 m-2 s3 cd sr,對頻率n = 540 × 1012赫茲之單色輻射光。倒過來看該關係,燭光的精確表達式係由定義常數Kcd、h和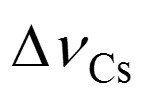 給出:
給出:
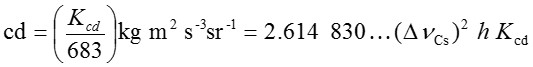
定義的效應為:1燭光為頻率540 × 1012赫茲之單色輻射光源,在給定方向發出之每立弳輻射通量為683分之1瓦特之發光強度。
定義常數之間的關係
以7個定義常數為基礎的基本單位新定義中,主要變更的單位為千克、安培、克耳文和莫耳,秒、米和燭光大致和現行的定義一樣,只是為了使7個新定義的表達形式一致,在敘述上作些修改,但實質並未改變。
定義更新後,基本單位和物理常數的關係之間的關連如下所述 (圖一):
1) 秒的定義依存於銫133超精細分裂頻率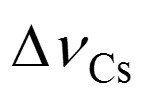 ;
;
2) 米的定義依存於光在真空中的速度c和銫133超精細分裂頻率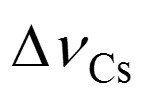 ;
;
3) 千克的定義依存於普朗克常數h、光速c和銫133超精細分裂頻率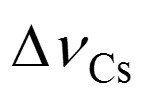 ;
;
4) 電流的定義依存於基本電荷常數e以及銫133超精細分裂頻率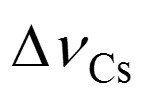 ;
;
5) 克耳文依存於波茲曼常數k普朗克常數h、光速c和銫133超精細分裂頻率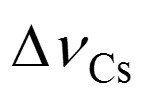 ;
;
6) 莫耳單獨依存於亞佛加厥常數NA;
7) 燭光依存於發光效能Kcd、普朗克常數h,光速c和銫133超精細分裂頻率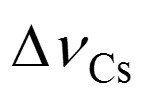 。
。
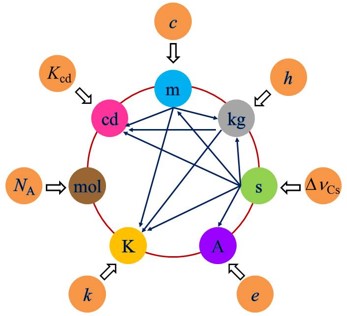
圖一 7個基本單位和物理常數的關係
基本單位定義的更新,將有助於改善基本單位實際實現的不確定度。
秒的不確定度仍維持在1 × 10-14,而米仍維持在2.5 × 10-8。
以定義常數為基礎的單位新定義完成後,最大的益處是基本單位不再依賴如國際千克原器之人工實物,實驗室只要有能力,都能以各定義常數為基準,實現各基本單位的定義。如同自1983年長度單位米的定義改以光速為基準後,只要能量測光頻率,任何實驗室都可以實現長度標準一樣。
結語
SI為一致的單位制,應用於國際貿易、高科技製造業、人類健康和安全,環境保護、全球氣候研究以及支援上述這些領域的基礎科學。SI係以目前科學家、技術人員和工程師所熟悉對物體本質的描述為基礎。自1960年第11屆CGPM正式定義並建立了SI之後,為因應使用者的要求與科技的進步,持續地作研究和修改。最近的修訂,或許是SI建立以來最明顯的一次,預定將於2018年由第26屆CGPM完成。
原本最佳的基本單位即應選取具唯一性、不變性、普遍性又容易實現的單位作為計量單位的基準。以國際千克原器IPK為例,雖具有唯一性和相當好的不變性,卻缺乏普遍性,又不變性也已被質疑。而新修訂之SI單位的定義則建立在一組7個定義常數之上,且這些定義常數的單位可以導出完整的單位制。物理常數就是具有唯一性、不變性、普遍性,而目前選取這7個定義常數,更是整個單位制定義上的基盤。
然而,採用這些涉及量子物理的7個基本單位之定義,並非每個NMI都有能力進行實際實現的工作。除了少數幾個科技先進、經費充裕的國家之外,能否普及至米制公約會員國,可能也是一個未來待克服的課題。
誌謝
本文感謝工業技術研究院量測技術發展中心副主任彭國勝博士熱心指導。
參考文獻
- BIPM, Drift of ninth SI Brochure, 11 December 2015.
- BIPM, Brochure of the International System of Units (SI), 8th Edition, 2006.
- BIPM, Supplement updates to 8th edition (2006) of the SI Brochure, 2014.
- 臼田 孝,2014,国際単位系 (SI) の体系紹介と最新動向 (概論),計測と制御Vol.53. No.1,2014年1月。
- Sandra Knotts, Peter J. Mohr, and William D. Phillips, An Introduction to the New SI , hysics Teachers,Vol. 55, January 2017.
- 經濟部標準檢驗局,2003,法定度量衡單位及其所用之倍數、分數之名稱、定義及代號。
- 陳兩興,2013 ~ 2015,國際單位制 (SI) 的基本單位介紹 (1~8),量測資訊,No.156 ~ No.166,2013年11月~ 2015年11月。
- 大岩彰等共著,きちんとわかる計量標準,独立行政法人産業技術総合研究所,2008年3月。
- Proposed redefinition of SI base units/Wikipedia, the free encyclopedia at: https://en.wikipedia.org/wiki/Proposed_redefinition_of_SI_base_units
- 松山裕,やさしい計量単位の話,財団法人省エネルギーセンター,1996年1月。
=========================================
作者簡介:陳兩興 / 工業技術研究院 量測技術發展中心 特約研究員
=========================================
